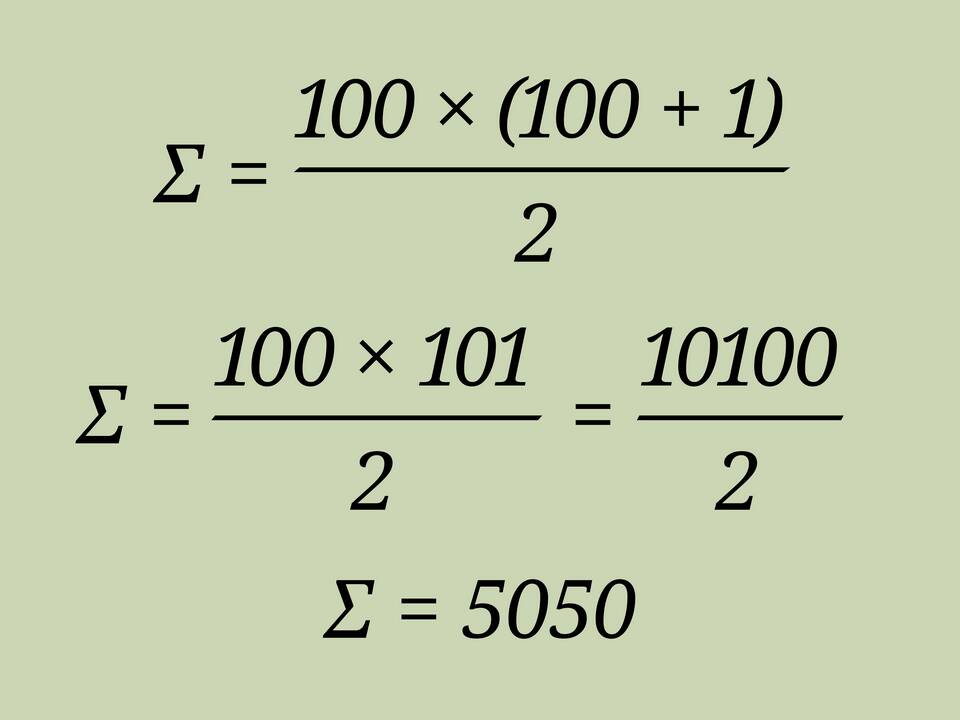Сумма целых чисел - это результат сложения последовательности целых чисел. В математике существует несколько важных случаев вычисления сумм целых чисел, которые имеют практическое значение.
Содержание
Сумма последовательных целых чисел
Для последовательности целых чисел от 1 до n сумма вычисляется по формуле:
| Формула | S = n(n + 1)/2 |
| Пример | Сумма чисел от 1 до 100: 100×101/2 = 5050 |
Сумма произвольного диапазона целых чисел
Для суммы целых чисел от a до b (где a ≤ b) формула имеет вид:
- S = (a + b)(b - a + 1)/2
- Пример: сумма от 10 до 15: (10+15)(15-10+1)/2 = 25×6/2 = 75
Свойства суммы целых чисел
- Коммутативность: a + b = b + a
- Ассоциативность: (a + b) + c = a + (b + c)
- Существование нулевого элемента: a + 0 = a
- Существование противоположного элемента: a + (-a) = 0
Сумма четных и нечетных чисел
| Тип чисел | Формула суммы |
| Первые n четных чисел | S = n(n + 1) |
| Первые n нечетных чисел | S = n² |
Применение сумм целых чисел
- В теории чисел и алгебре
- В комбинаторике и теории вероятностей
- В компьютерных алгоритмах
- В физических и экономических расчетах
Понимание принципов вычисления сумм целых чисел является фундаментальным для дальнейшего изучения математики и ее приложений в различных областях науки и техники.