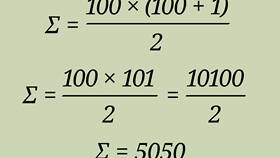В математике понятие "сумма разности" может иметь несколько интерпретаций в зависимости от контекста. Рассмотрим основные варианты понимания этого выражения и их практическое применение.
Содержание
В математике понятие "сумма разности" может иметь несколько интерпретаций в зависимости от контекста. Рассмотрим основные варианты понимания этого выражения и их практическое применение.
Основные трактовки понятия
1. Сумма разностей между элементами
В данном случае подразумевается операция последовательного вычитания элементов с последующим суммированием полученных результатов:
- Для двух чисел: (a - b) + (b - a) = 0
- Для последовательности: Σ(xᵢ - xᵢ₊₁) от i=1 до n-1
2. Разность сумм
Часто под "суммой разности" понимают разность между двумя суммами:
- (Σaᵢ) - (Σbᵢ) = Σ(aᵢ - bᵢ)
- Применяется в статистике для сравнения групп данных
Математические свойства
| Свойство | Формула | Пример |
| Коммутативность | Σ(aᵢ - bᵢ) ≠ Σ(bᵢ - aᵢ) | (5-3)+(2-1)=3 ≠ (3-5)+(1-2)=-3 |
| Ассоциативность | Σ(aᵢ - bᵢ - cᵢ) = Σ(aᵢ - (bᵢ + cᵢ)) | (10-2-3)+(5-1-2)=7 |
| Дистрибутивность | kΣ(aᵢ - bᵢ) = Σ(kaᵢ - kbᵢ) | 2[(4-1)+(3-2)]=8 = [(8-2)+(6-4)]=8 |
Практические применения
В финансовых расчетах
- Расчет совокупных отклонений показателей
- Анализ разницы между плановыми и фактическими значениями
- Определение суммарных изменений во временных рядах
В статистике
- Вычисление среднего линейного отклонения
- Анализ вариаций данных
- Сравнение выборок
Примеры вычислений
Пример 1: Простая сумма разностей
Даны пары чисел: (5,2), (8,3), (10,6)
Сумма разностей: (5-2) + (8-3) + (10-6) = 3 + 5 + 4 = 12
Пример 2: Разность сумм
Даны два набора чисел: A={2,4,7}, B={1,3,5}
Разность сумм: (2+4+7) - (1+3+5) = 13 - 9 = 4
Сумма попарных разностей: (2-1)+(4-3)+(7-5) = 1+1+2 = 4
Пример 3: Телескопическая сумма
Σ(1/n - 1/(n+1)) от n=1 до N = 1 - 1/(N+1)
При N→∞ сумма стремится к 1
Важные особенности
- Порядок операций существенно влияет на результат
- В конечных суммах можно менять порядок слагаемых
- Для бесконечных рядов требуется проверка сходимости
- В вероятностных расчетах используется понятие математического ожидания разности
Понимание принципов работы с суммами разностей является важным инструментом в различных областях математики, статистики и прикладных наук. Правильное применение этих операций позволяет анализировать изменения и отклонения в данных, решать практические задачи сравнения и оценки различий.
